A.I. Wiki

A Beginner’s Guide to Important Topics in AI, Machine Learning, and Deep Learning.

A Beginner's Guide to Markov Chain Monte Carlo, Machine Learning & Markov Blankets

Markov Chain Monte Carlo is a method to sample from a population with a complicated probability distribution.

Let’s define some terms:

  • Sample - A subset of data drawn from a larger population. (Also used as a verb to sample; i.e. the act of selecting that subset. Also, reusing a small piece of one song in another song, which is not so different from the statistical practice, but is more likely to lead to lawsuits.) Sampling permits us to approximate data without exhaustively analyzing all of it, because some datasets are too large or complex to compute. We’re often stuck behind a veil of ignorance, unable to gauge reality around us with much precision. So we sample.1
  • Population - The set of all things we want to know about; e.g. coin flips, whose outcomes we want to predict. Populations are often too large for us to study them in toto, so we sample. For example, humans will never have a record of the outcome of all coin flips since the dawn of time. It’s physically impossible to collect, inefficient to compute, and politically unlikely to be allowed. Gathering information is expensive. So in the name of efficiency, we select subsets of the population and pretend they represent the whole. Flipping a coin 100 times would be a sample of the population of all coin tosses and would allow us to reason inductively about all the coin flips we cannot see.
  • Distribution (or probability distribution) - You can think of a distribution as table that links outcomes with probabilities. A coin toss has two possible outcomes, heads (H) or tails (T). Flipping it twice can result in either HH, TT, HT or TH. So let’s contruct a table that shows the outcomes of two coin tosses as measured by the number of H that result. Here’s a simple distribution:
Number of H -   Probability
0   0.25
1   0.50
2   0.25

There are just a few possible outcomes, and we assume H and T are equally likely. Another word for outcomes is states, as in: what is the end state of the coin flip?

Instead of attempting to measure the probability of states such as heads or tails, we could try to estimate the distribution of land and water over an unknown earth, where land and water would be states. Or the reading level of children in a school system, where each reading level from 1 through 10 is a state.

Markov Chain Monte Carlo (MCMC) is a mathematical method that draws samples randomly from a black box to approximate the probability distribution of attributes over a range of objects or future states. You could say it’s a large-scale statistical method for guess-and-check.

MCMC methods help gauge the distribution of an outcome or statistic you’re trying to predict, by randomly sampling from a complex probabilistic space.

As with all statistical techniques, we sample from a distribution when we don’t know the function to succinctly describe the relation to two variables (actions and rewards). MCMC helps us approximate a black-box probability distribution.

With a little more jargon, you might say it’s a simulation using a pseudo-random number generator to produce samples covering many possible outcomes of a given system.

Learn to use AI in Simulations »

Concrete Examples of Monte Carlo Sampling

Let’s say you’re a gambler in the saloon of a Gold Rush town and you roll a suspicious die without knowing if it is fair or loaded. To test it, you roll a six-sided die a hundred times, count the number of times you roll a four, and divide by a hundred. That gives you the probability of four in the total distribution. If it’s close to 16.7 (1/6 * 100), the die is probably fair.

Monte Carlo looks at the results of rolling the die many times and tallies the results to determine the probabilities of different states. It is an inductive method, drawing from experience. The die has a state space of six, one for each side.

The states in question can vary. Instead of games of chance, the states might be letters in the Roman alphabet, which has a state space of 26. (“e” happens to be the most frequently occurring letter in the English language….) They might be stock prices, weather conditions (rainy, sunny, overcast), notes on a scale, electoral outcomes, or pixel colors in a JPEG file. These are all systems of discrete states that can occur in seriatim, one after another. Here are some other ways Monte Carlo is used:

  • In finance, to model risk and return
  • In search and rescue, the calculate the probably location of vessels lost at sea
  • In AI and gaming, to calculate the best moves (more on that later)
  • In computational biology, to calculate the most likely evolutionary tree (phylogeny)
  • In telecommunications, to predict optimal network configurations

Rolling a die is a one-step process, and running a Monte Carlo on a six-sided die is pretty simple. But Monte Carlo experiments can also test strategies, or sequential decision-making protocols based on different predictive models, which by definition must take many steps over time.

Imagine a checkers player looking ahead a certain number of moves from any given state of the board. For each move that is one step out, she will need to imagine several likely responses from her opponent, as well as her answer to those moves, and so on. The branches grow in number very quickly on that tree of moves. The distribution of all wins and losses based on her strategy as it applies to her opponent’s responses would be the Monte Carlo results for that strategy. A different player, with a different strategy, would produce another set of wins and losses that could be contrasted with the first. That’s how MCMC is used to validate ML models.

Systems and States

On a more abstract level, a system is a set of things connected together by different mechanisms, processes and means of communication. You can represent it as a graph, where each state is a vertex or node, and each transition is an edge. But what are nodes?

  • Cities on a map are nodes. A road trip strings them together in transitions. The map represents the system.
  • Words in a language are nodes. A sentence is just a series of transitions from word to word.
  • Genes on a chromosome are nodes. To read them (and to create amino acids) is to go through their transitions.
  • Web pages on the Internet are nodes. Links are the transitions. That’s the basis of PageRank.
  • Bank accounts in a financial system are nodes. Transactions are the transitions.
  • Emotions are states in a dynamic psychological system. Mood swings are the transitions.
  • Social media profiles are nodes in the network. Follows, likes, messages and friending are the transitions. This is the basis of link analysis.
  • Rooms in a house are nodes. Doorways are the transitions.

A graph can also represent the set of states for a dynamic system, where each state is a condition of that system.

So nodes, or states, are an abstraction used to describe these discrete, separable, things. A group of those states bound together by transitions is a system. And those systems have structure, in that some states are more likely to occur than others (ocean, land), or that some states are more likely to follow others.

For example, we are more likely to read the sequence Paris -> France than Paris -> Texas, although both sequences exist, just as we are more likely to drive from Los Angeles to Las Vegas than from L.A. to Slab City, even though both places are nearby.

A list of all possible states is known as the “state space.” The more states you have, the larger the state space gets, and the more complex your combinatorial problem becomes when you try to calculate transitions from state to state.

Markov Chains

Since states can occur one after another, it may make sense to traverse the state space, moving from one to the next. A Markov chain is a probabilistic way to traverse a system of states. It traces a series of transitions from one state to another. It’s a random walk across a graph.

Each current state may have a set of possible future states that differs from any other. For example, you can’t drive straight from Georgia to Oregon - you’ll need to hit other states, in the double sense, in between. We are all, always, in such corridors of probabilities; from each state, we face an array of possible future states, which in turn offer an array of future states that are two degrees away from the start, changing with each step as the state tree unfolds. New possibilites open up, others close behind us. Since we generally don’t have enough compute to explore every possible state of a game tree for complex games like Go, one trick that organizations like DeepMind use is Monte Carlo Tree Search to narrow the beam of possibilities to only those states that promise the most likely reward.

Traversing a Markov chain, you’re not sampling with a God’s-eye view any more like a conquering alien. You are in the middle of things, groping your way toward one of several possible future states, step by probabilistic step, through a Markov Chain.2

While our journeys across a state space may seem unique, like road trips across America, an infinite number of road trips would slowly give us a picture of the country as a whole, and the network that links its cities and states together. This is known as an equilibrium distribution. That is, given infinite random walks through a state space, you can come to know how much total time would be spent in any given state in the space. If this condition holds, you can use Monte Carlo methods to initiate randoms “draws”, or walks through the state space, in order to sample it. That’s MCMC.

On Markov Time

Markov chains have a particular property: oblivion. Forgetting.

They have no long-term memory. They know nothing beyond the present, which means that the only factor determining the transition to a future state is a Markov chain’s current state.

Markov Chains assume the entirety of the past is encoded in the present, so we don’t need to know anything more than where we are to infer where we will be next.3

For an excellent interactive demo of Markov Chains, see the visual explanation on this site.

So imagine the current state as the input data, and the distribution of attributes related to those states (perhaps that attribute is reward, or perhaps it is simply the most likely future states), as the output. From each state in the system, by sampling you can determine the probability of what will happen next, doing so recursively at each step of the walk through the system’s states.

Markov Blankets: Life’s organizing principle?

An idea closely related to the Markov chain is the Markov blanket.

Let’s start from the top: A Markov chain steps from one state to the next, as though following a single thread. It assumes that everything it needs to know is encoded in the present state. Like humans, an agent moving through a Markov chain has only the present moment to refer to, and the past only makes itself known in the present through the straggling relics that have survived the holocaust of time, or through the wormholes of memory. Based only on the present state, we can seek to predict the next state.

Markov blankets formulate the problem differently. First, we have the idea of a node in a graph. That node is the thing we want to predict, and other nodes in the graph that are connected to the node in question can help us make that prediction. Those input nodes are a way of represent features as discrete and independent variables, rather than aggregating them into states.

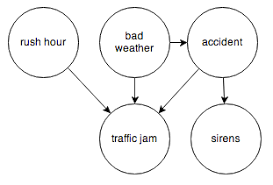
probabilistic graph

In a Bayesian network, the probability of some nodes depends on other nodes upstream from them in the graph, which are sometimes causal.

A Markov blanket makes the Markovian assumption that all you need to know in order to make a prediction about one node is encoded in the neighboring nodes it depends on.4

In a sense, a Markov blanket extends a two-dimensional Markov chain into a folded, three-dimensional field, and everything that affects a given node must first pass through that blanket, which channels and translates information through a layer.

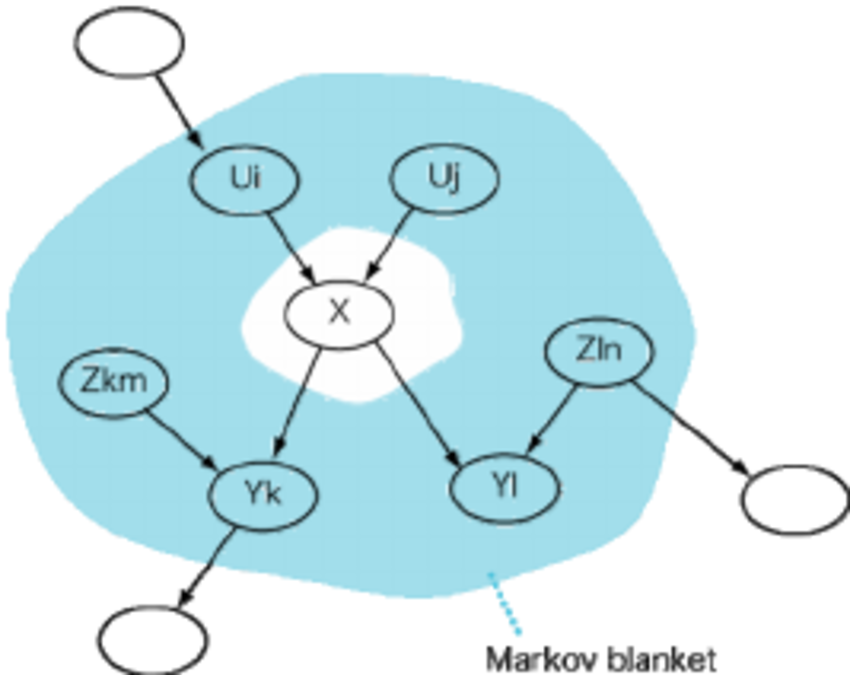
Markov blanket

So where are Markov blankets useful? Well, living organisms, first of all. All your sensory organs from skin to eardrums act as a Markov blanket wrapping your meat and brains in a layer of translation, through which all information must pass. In order to determine your inner state, all you really need to know is what’s passing through the nodes of that translation layer. Your sensory organs are a Markov blanket. Semi-permeable membranes act as Markov blankets for living cells. You might say that the traditional media such as newspapers and TV, and social media such as Facebook, operate as a Markov blanket for cultures and societies.

The term Markov blanket was coined by southern California’s great thinker of causality, Judea Pearl. Markov blankets play an important role in the thought of Karl Friston, who proposes that the organizing principle of life is that entities contained within a Markov blanket seek to maintain homeostasis by minimizing “free energy”, aka uncertainty, the gap between what they imagine, and what’s happening according to the signals coming through their Markov blanket.5

When differences arise between their internal model of the world, and the world itself, they can either 1) move their internal model closer to the new data, much as machine learning models adjusts their parameters; 2) act on the world to move it closer to what they imagine it to be (move the data closer to their internal model); or 3) pretend that their model conforms to reality and keep watching cable news.

Probability as Space

It’s actually useful to visualize “state space” as space, just like you might picture land and water spread over a larger map, each one of them a probability as much as they are a physical thing, from MCMC’s point of view. Unfold a six-sided die and you have a flattened state space in six equal pieces, shapes on a plane. Line up the letters by their frequency for 11 different languages, and you get 11 different state spaces:

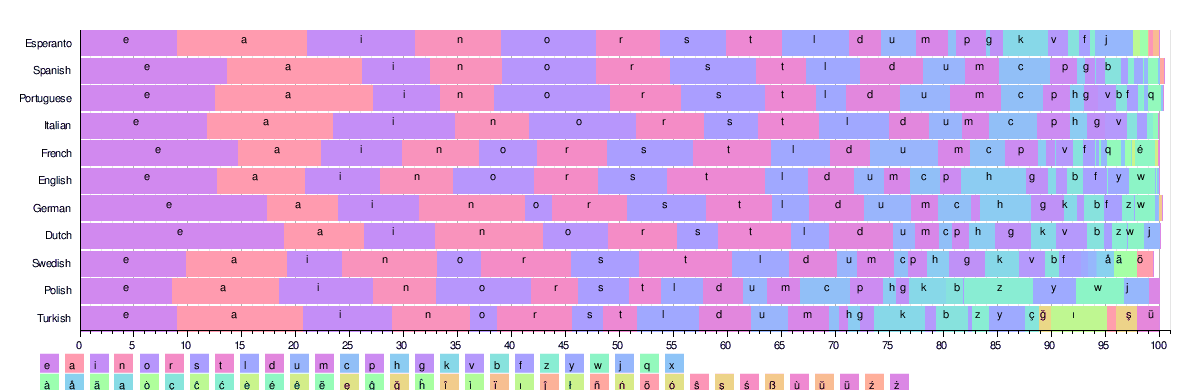
letter frequency

Five letters account for half of all characters occurring in Italian, but only a third of Swedish.

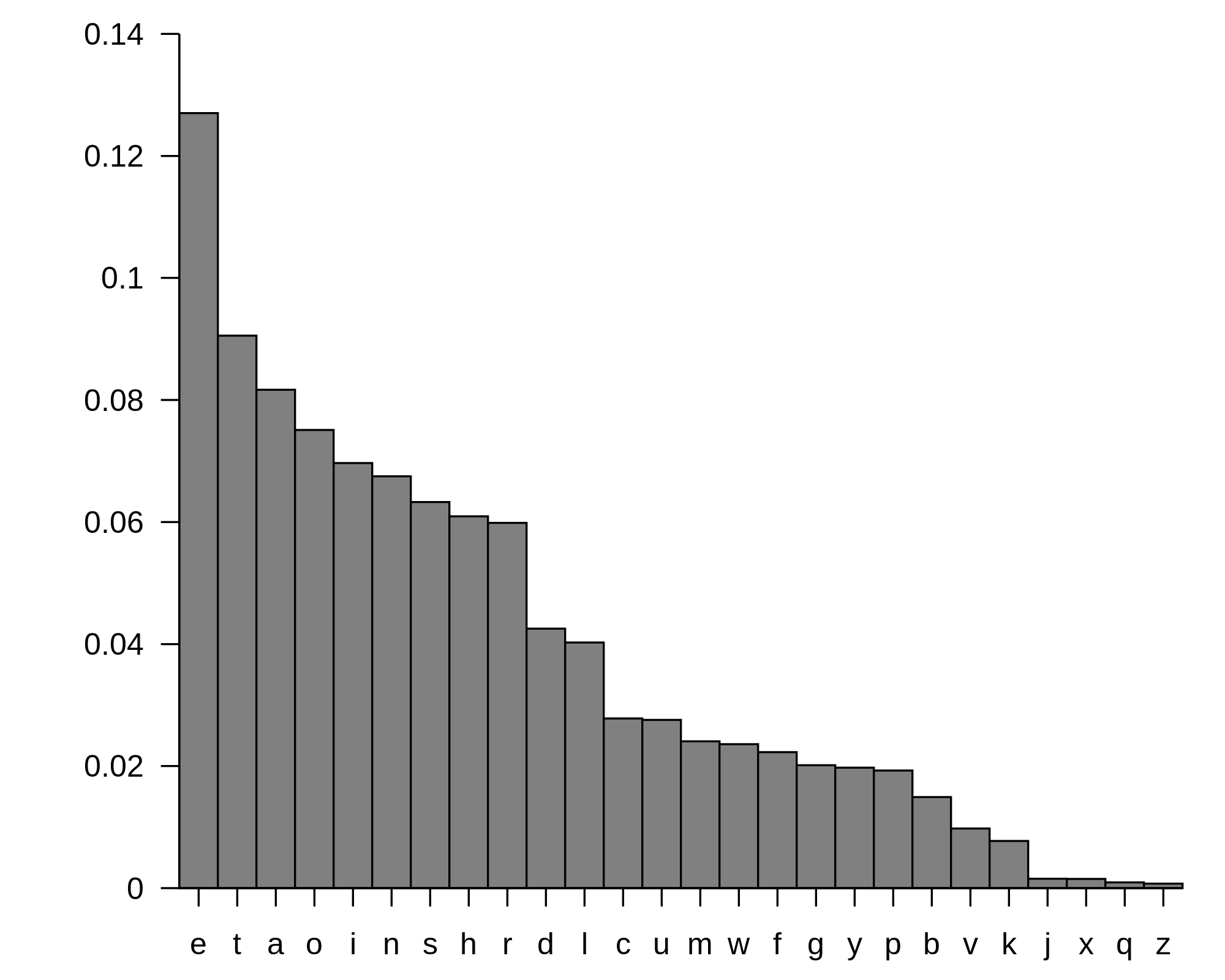
If you wanted to look at the English language alone, you would get this set of histograms. Here, probabilities are defined by a line traced across the top, and the area under the line can be measured with a calculus operation called integration, the opposite of a derivative.

english letter distribution

MCMC and Deep Reinforcement Learning

MCMC can be used in the context of simulations and deep reinforcement learning to sample from the array of possible actions available in any given state.

That is, Monte Carlo experiments are useful in comparing the performance of different optimizers, or strategies, over a distribution of possible states in an operational system; i.e. running Monte Carlo’s on both linear programming and deep reinforcement learning can show you how they both perform when applying their respective strategies to the same system.

For more information, please see our pages on Deep Reinforcement Learning and Simulation & AI.

Further Reading on Markov Chain Monte Carlo

Footnotes

1) You could say that life itself is too complex to know in its entirety, confronted as we are with imperfect information about what’s happening and the intent of others. You could even say that each individual human is a random draw that the human species took from the complex probability distribution of life, and that we are each engaged in a somewhat random walk. Literature is one way we overcome the strict constraints on the information available to us through direct experience, the limited bandwidth of our hours and sensory organs and organic processing power. Simulations mediated by books expose us to other random walks and build up some predictive capacity about states we have never physically encountered. Which brings us to the fundamental problems confronted by science: How can we learn what we don’t know? How can we test what we think we know? How can we say what we want to know? (Expressed that in a way an algorithm can understand.) How can we guess smarter? (Random guesses are pretty inefficient…)

2) Which points to a fundamental truth: Time and space are filters. In his book The Master Algorithm, Pedro Domingo quotes an unnamed wag as saying “Space is the reason that everything doesn’t happen to you.” Memory is how we overcome the filter of time, and technology is how we overcome, or penetrate, the filter of space.

3) It’s interesting to think about how these ways of thinking translate, or fail to translate, to real life. For example, while we might agree that the entirety of the past is encoded in the present moment, we cannot know the entirety of the present moment. The walk of any individual agent through life will reveal certain elements of the past at time step 1, and others at time step 10, and others still will not be revealed at all because in life we are faced with imperfect information – unlike in Go or Chess. Recurrent neural nets are structurally Markovian, in that the tensors passed forward through their hidden units contain everything the network needs to know about the past. LSTMs are thought to be more effective at retaining information about a larger state space (more of the past), than other algorithms such as Hidden Markov Models; i.e. they decrease how imperfect the information is upon which they base their decisions.

4) *Fwiw, the blanket actually encompasses the upstream nodes that influence the node you want to predict, as well as all the nodes directly influencing the child nodes of the node you want to predict. *

5) So a living being reduces the uncertainty around it by both exploring the world and acting upon it in order to make it conform and support its long-term homeostatis. Well, what if one organism’s power translates to another organisms uncertainty, and we’re playing a zero-sum game with free energy? Can we explain geopolitics with Markov blankets? Friston’s followers have applied the idea to almost everything else, so why not…

5) An origin story: “While convalescing from an illness in 1946, Stan Ulam was playing solitaire. It occurred to him to try to compute the chances that a particular solitaire laid out with 52 cards would come out successfully (Eckhard, 1987). After attempting exhaustive combinatorial calculations, he decided to go for the more practical approach of laying out several solitaires at random and then observing and counting the number of successful plays. This idea of selecting a statistical sample to approximate a hard combinatorial problem by a much simpler problem is at the heart of modern Monte Carlo simulation.”

Further Reading

Chris V. Nicholson

Chris V. Nicholson is a venture partner at Page One Ventures. He previously led Pathmind and Skymind. In a prior life, Chris spent a decade reporting on tech and finance for The New York Times, Businessweek and Bloomberg, among others.