Decision Tree

A decision tree is a series of nodes, a directional graph that starts at the base with a single node and extends to the many leaf nodes that represent the categories that the tree can classify. Another way to think of a decision tree is as a flow chart, where the flow starts at the root node and ends with a decision made at the leaves. It is a decision-support tool. It uses a tree-like graph to show the predictions that result from a series of feature-based splits.

Here are some useful terms for describing a decision tree:

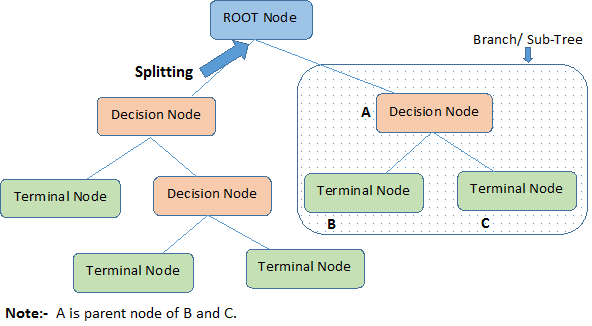
• Root Node: A root node is at the beginning of a tree. It represents entire population being analyzed. From the root node, the population is divided according to various features, and those sub-groups are split in turn at each decision node under the root node.
• Splitting: It is a process of dividing a node into two or more sub-nodes.
• Decision Node: When a sub-node splits into further sub-nodes, it’s a decision node.
• Leaf Node or Terminal Node: Nodes that do not split are called leaf or terminal nodes.
• Pruning: Removing the sub-nodes of a parent node is called pruning. A tree is grown through splitting and shrunk through pruning.
• Branch or Sub-Tree: A sub-section of decision tree is called branch or a sub-tree, just as a portion of a graph is called a sub-graph.
• Parent Node and Child Node: These are relative terms. Any node that falls under another node is a child node or sub-node, and any node which precedes those child nodes is called a parent node.

Decision trees are a popular algorithm for several reasons:

• Explanatory Power: The output of decision trees is interpretable. It can be understood by people without analytical or mathematical backgrounds. It does not require any statistical knowledge to interpret them.
• Exploratory data analysis: Decision trees can enable analysts to identify significant variables and important relations between two or more variables, helping to surface the signal contained by many input variables.
• Minimal data cleaning: Because decision trees are resilient to outliers and missing values, they require less data cleaning than some other algorithms.
• Any data type: Decision trees can make classifications based on both numerical and categorical variables.
• Non-parametric: A decision tree is a non-parametric algorithm, as opposed to neural networks, which process input data transformed into a tensor, via tensor multiplication using large number of coefficients, known as parameters.

Learn to build AI in Simulations »

Disadvantages

• Overfitting: Over fitting is a common flaw of decision trees. Setting constraints on model parameters (depth limitation) and making the model simpler through pruning are two ways to regularize a decision tree and improve its ability to generalize onto the test set.
• Predicting continuous variables: While decision trees can ingest continuous numerical input, they are not a practical way to predict such values, since decision-tree predictions must be separated into discrete categories, which results in a loss of information when applying the model to continuous values.
• Heavy feature engineering: The flip side of a decision tree’s explanatory power is that it requires heavy feature engineering. When dealing with unstructured data or data with latent factors, this makes decision trees sub-optimal. Neural networks are clearly superior in this regard.

One weird thing about decision trees (or random forests) is how conceptually simple they are, while in terms of implementation they’re non-trivial. How do you find the optimal split/feature based on entropy? Naively implemented, they require something on the order of O(kNlogN) for each split. Multiply that by the number of leaves (2^depth), and multiply that by the number of trees in your forest.

Further Reading

• Introduction to Random Forests and Decision Trees